دانلود شبیه سازی تبدیل فوریه در نرم افزار متلب (بررسی کاملا تخصصی)
تبدیل فوریه، ابزاری است که یک شکل موج (یک تابع یا سیگنال) را به یک شکل دیگر، مشخص شده بوسیله توابع سینوسی و کسینوسی، تفکیک می کند. تبدیل فوریه نشان می دهد که هر شکل موج را می توان به صورت حاصلجمع توابع سینوسی بازنویسی کرد. در این پروژه، شبیه سازی تبدیل فوریه و یک سری از توابع مختلط، توابع فوریه فرکانسی و فازی با نرم افزار متلب انجام شده است. جزئیات و توضیحات هر کدام از کدها و دستورات داخل برنامه ها مشخص شده اند.

| گزارشکار: ندارد | شبیه سازی : دارد (6 ام فایل متلب) |
تبدیل فوریه در MATLAB
تبدیل فوریه (FT)، یک تابع زمانی (یک سیگنال) را به فرکانس های تشکیل دهنده آن، تجزیه می کند. این تبدیل مشابه با یک تار موسیقی عمل می کند که آنرا می توان برحسب حجم (بزرگی) و فرکانس نت های تشکیل دهنده اش، بیان نمود. اصطلاح تبدیل فوریه، به هر دوی نمایش حوزه فرکانسی و عملیات های ریاضیاتی مرتبط دهنده نمایش حوزه فرکانس به یک تابع حوزه زمانی، اشاره دارد. تبدیل فوریه یک تابع زمانی، خودش یک تابع مقدار مختلط از فرکانس است که بزرگی (ضریب یا مادول) آن، نشان دهنده مقداری است که آن فرکانس در تابع اصلی نشان می دهد و آرگومان آن، اختلاف فاز موج سینوسی پایه در آن فرکانس است. تبدیل فوریه به توابع زمانی محدود نیست، اما حوزه تابع اصلی را معمولاً حوزه زمانی می گویند. همچنین یک تبدیل فوریه معکوس وجود دارد که به زبان ریاضی، تابع اصلی را از نمایش حوزه فرکانسی آن، تولید و سنتز می کند.
عملیات های خطی انجام شده در یک حوزه (زمانی یا فرکانسی) عملیات های متناظر در حوزه های دیگر، که گاهی انجامشان آسان تر است، دارند. عملیات مشتق گیری در حوزه زمانی متناظر است با حاصلضرب در فرکانس، بنابراین تحلیل تعدادی معادلات دیفرانسیل در حوزه فرکانس، آسان تر است. همچنین، کانولوشن در حوزه زمانی متناظر با حاصلضرب عادی در حوزه فرکانس است. بعد از انجام عملیات های مطلوب، تبدیل مجدد نتیجه به حوزه زمانی قابل انجام است. تحلیل هارمونیک، مطالعه سیستماتیک و نظاممند رابطه بین حوزه های فرکانس و زمانی است و شامل انواع توابع یا عملیات هایی است که به نحوی «ساده تر» هستند و اتصالات و ارتباطات عمیق با زمینه های بسیاری از ریاضیات مدرن دارند.
توابعی که در حوزه زمانی محدود و موضعی هستند، تبدیل فوریه هایی دارند که در حوزه فرکانس گسترش یافته اند و بالعکس و این پدیده ای است که به آن اصل عدم قطعیت گفته می شود. حالت بحرانی برای این اصل، تابع گاوسی است که از اهمیتی اساسی در نظریه احتمالات و آمار و همچنین در مطالعه پدیده های فیزیکی که توزیع نرمال دارند (برای مثال، گسیل (diffusion)، برخوردارند. تبدیل فوریه یک تابع گاوسی، یک تابع گاوسی دیگر است. جوزف فوریه، این تبدیل را در مطالعه انتقال حرارت معرفی کرد، به این صورت که توابع گاوسی به صورت جواب های معادله حرارت پدیدار شوند.
این شبیه سازی با استفاده از نرم افزار متلب انجام شده و توضیحات مربوط به کدها نیز در هر برنامه اشاره شده است. در ادامه تعدادی از نتایج خروجی برنامه قرار داده شده اند.
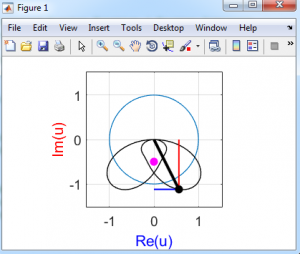

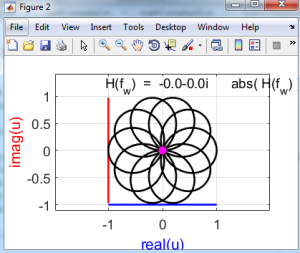
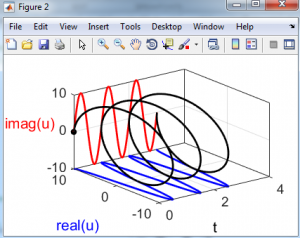
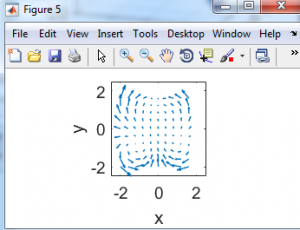

دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.