دانلود شبیه سازی مقاله جداسازی منبع کور و تحلیل اجزای پراکنده در ترکیب های بیش از حد کامل
| عنوان فارسی |
جداسازی منبع کور و تجزیه و تحلیل اجزای پراکنده در ترکیب های بیش از حد کامل |
| عنوان انگلیسی |
Blind source separation and sparse component analysis of overcomplete mixtures |
| کلمات کلیدی |
جداسازی منبع کور؛ ماتریس های پراکنده؛ تحلیل اجزای مستقل؛ معادلات؛ پردازش سیگنال زیست پزشکی؛ داده کاوی؛ بیوفیزیک؛ تحلیل آماری |
| درسهای مرتبط |
پردازش سیگنال |
| تعداد صفحات انگلیسی : 4 | نشریه : IEEE |
| سال انتشار : 2004 | تعداد رفرنس مقاله : 10 |
| فرمت مقاله انگلیسی : PDF | نوع مقاله : ISI |
| آیا این مقاله برای بیس پایان نامه مناسب است؟ : بله | آیا این مقاله برای ارائه کلاسی مناسب است؟ : بله |
| برنامه ای که در آن مقاله شبیه سازی شده است : این مقاله در محیط متلب پیاده سازی شده است | نام مجله مقاله : International Conference on Acoustics, Speech, and Signal Processing (ICASSP) (کنفرانس بین المللی آکوستیک، گفتار و پردازش سیگنال (ICASSP)) |
| ترجمه: ندارد | گزارشکار : ندارد | شبیه سازی : دارد (فایل های شبیه سازی در متلب با فرمت .m) |
این مقاله در محیط متلب به صورت کامل شبیه سازی شده و در صورت خرید و دانلود مقاله شما به راحتی قادر خواهید بود از برنامه مربوطه استفاده نمایید. در صورت بروز هر گونه مشکل در نحوه ی اجرای برنامه سایت سیگمالند به مدت 24 ساعت بعد از خرید محصول، پشتیبانی آن را تا اجرای کامل برعهده دارد.
پروژه متلب جداسازی منبع کور (BSS)
در این پروژه، شرایط (شرایط k-SCA ) را تدوین می کنیم که تحت آن می توانیم یک ماتریس (m/spl بار/N) ، X، (مجموعه داده ها) را به طور مجزا (تا مقیاس بندی و جایگشت) به عنوان ضرب ماتریس های m/spl بار/n و n/spl بار/N، A و S، (اغلب به ترتیب به عنوان ماتریس اختلاط یا واژه نامه و ماتریس منبع نامیده می شود) ارائه دهیم. به گونه ای که S از سطح n-m+k پراکنده است، که به این معناست که هر ستون S دارای حداقل n-m+k عنصر صفر است. از اینرو آنرا مسئله و تحلیل مؤلفههای k-sparse (k-SCA) نامگذاری می کنیم. همچنین، شرایط یک ماتریس، S، به صورتی ارائه شده است که شرایط k-SCA برای ماتریس X=AS، که در آن A یک ماتریس دلخواه از برخی گروه ها است، برآورده می شود. این قضیه، مسئله جداسازی کور منبع است و شرایط فوق، شرایط شناسایی نامیده می شود. همچنین در این پروژه، الگوریتمهای جدیدی را برای شناسایی ماتریس (تحت شرایط k-SCA)، و برای بازیابی منبع (تحت شرایط شناسایی) ارائه می دهیم. علاوه بر این، در این مقاله، روشها با مثالهایی نشان داده شدهاند که تفکیک خوبی از بخش فرکانس بالای ترکیبی از تصاویر را پس از پراکندگی مناسب نشان میدهند.
در این مقاله با قاطعیت نظریه ای را برای تفکیک و جداسازی سیگنال کور از ترکیبات خطی فراکامل سیگنال های پراکنده ایجاد نمودیم، عبارات کافی مربوط به آن را ارائه نموده و الگوریتم های جدیدی را نیز برای شناسایی ماتریس اختلاط و بازیابی منبع ایجاد نمودیم. مفروضات اصلی برای پراکندگی (یعنی هر ستون از ماتریس منبع دارای عناصر غیرصفر کمتری نسبت به بعد اختلاط است)، این امکان را فراهم می کند تا برای بازیابی منبع توسط الگوریتم خود، یگانگی را بدست آوریم. آزمایش ارائه شده برای تفکیک سیگنالهای ایجاد شده مصنوعی با سطح پراکندگی کافی، نتایج بسیار خوبی را ارائه می دهد. همچنین آزمایشات انجام شده برای تفکیک ترکیبات تصاویر در حالت کامل، بسیار خوب هستند و در حالت فراکامل (به دلیل وجود اجزای فرکانس پایین) به قدر کافی از عملکرد خوبی برخوردار هستند.
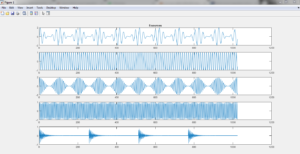
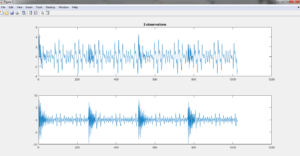
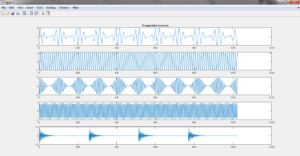
این شبیه سازی در محیط نرم افزار متلب (MATLAB) انجام شده و در ادامه نیز تصاویر مربوط به خروجی های شبیه سازی قرار داده شده است:





دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.